Hopefully this post will make the paper a little more accessible. I'm writing it for anyone who might ever ponder getting a tattoo of a yin-yang symbol, but who may also want to take the expression of balance a little deeper. For those who've already inked themselves, fret not because I'll present some rationale at the end suggesting the more familiar symbol is just as deeply balanced (in a meta sense at least).
Here are two candidate representations for an ideal yin-yang symbol...
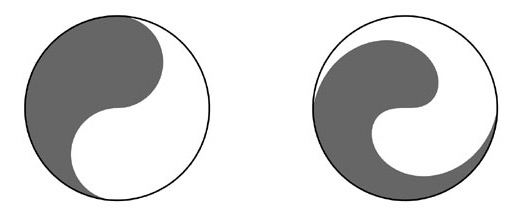 The light/dark boundary line of the first is made from two semi-circles. The latter is the alternative suggested in the paper, having a boundary based on Fermat's spiral. Both symbols have the symmetry that half of the area of the disk is light and half is dark. And both boundaries have a rotational symmetry - you can rotate the curve 180 degrees and it remains unchanged (though such a rotation of the disk does swap the light/dark areas).
The light/dark boundary line of the first is made from two semi-circles. The latter is the alternative suggested in the paper, having a boundary based on Fermat's spiral. Both symbols have the symmetry that half of the area of the disk is light and half is dark. And both boundaries have a rotational symmetry - you can rotate the curve 180 degrees and it remains unchanged (though such a rotation of the disk does swap the light/dark areas).I'd like to share a quote from the paper that goes to the heart of the argument, but will need to clarify a few terms they use first.
- They label the disk D and specify it has an area equal to 1.
- The area they call A can be taken to be either half of the yin-yang symbol based on Fermat's spiral, and has area 1/2.
- 'axial symmetry' means a reflection about an axis in the plane of the disk and going through the disk center1.
- By 'measure', they mean area. (The fancy term is Lebesgue measure.)
- By 'symmetric subset', they mean any subset of A that is fully the same color before and after a given reflection of the disk.
... we discovered a magic difference of the plane disk ... it contains a set AThe paper actually proves that a yin-yang symbol based on Fermat's spiral is the only one with this more subtle symmetry2. In this sense then, the symbol on the right has deeper symmetries than the one on the left.D of measure 1/2 all whose symmetric subsets have measure at most 1/4. Let us call such an A perfect. Any perfect set A has a remarkable property: For every axial symmetry s of D, the maximum subset of A symmetric with respect to s has measure 1/4. In words admitting far-going esoteric interpretations, perfect sets demonstrate a sharp equilibrium between their "symmetric" and "asymmetric" parts, whatever particular symmetry s is considered.
I wanted to see what the symmetric and asymmetric subsets of A looked like, so I wrote a short POV-Ray script to make an animation which runs through all the axial symmetries. For each symmetry, it reflects the darker half of the symbol as a lighter area, and the interaction of these two areas end up demarking the "maximum symmetric subsets" of A. For A taken to be the dark half, these are the darkest areas of intersection in the video.
If you pause the video, you'll be able to study the maximum symmetric subset with respect to a particular disk symmetry s. It's neat to note this subset is actually the union of two smaller disjoint sets, that is it is made up of two disconnected parts. This is also true for the corresponding asymmetric subset (a welcome "symmetry" of a different kind).
One property I find more "symmetric" about the prevalent semicircle yin-yang boundary is that it is tangent to the the outer disk. This is not true for Fermat's spiral (close but no cigar). I think it is often inevitable that to gain symmetry in one sense, you have to give it up in another seemingly disparate sense.
So having noted that, I'll close with the thought that maybe these two symbols are themselves foils for each other, faintly analogous to the dark/light areas of a single yin-yang. Perhaps they should not or could not exist in isolation to each other. In other words, you don't need to regret that tattoo in the small of your back :)
1 The imperfections of wikipedia led me astray in this. Their axial symmetry page
2 There are other perfect sets A of a disk, but the candidate yin-yang curves considered also arguably must manifest some other qualities of yin-yangness, so glossed over was that only Fermat's spiral has all those qualities in addition to cutting the disk into perfect sets.




Hello!
ReplyDeleteMy name is Maria, and I am from Lviv, Ukraine, so sorry my vary bad English.
Now I am cooperating with one of the authors "Fermat's Spiral and the Line Between Yin and Yang".
Can you sent me this video? It is very important for me.
Thanking you in anticipation.
My e-mail- maria-koroliyk@rambler.ru
Dear Maria,
ReplyDeleteI uploaded the video I made to www.gravitation3d.com/roice/video/yinyang.mp4 so that you can download it for your use. If I can help with any changes you might need, please let me know. It is easy for me to increase the size or quality, change the amount of transparency, alter colors, etc.
All the best,
Roice
I didn't follow or even try to follow all of that but I'll just say that I may prefer the new version better because the standard one always bothers me slightly with what appears to be a discontinuity at the center. There appears to be a sharp corner where the curve changes direction in the middle whereas it seems to be absent in the new version. Maybe the discontinuity is only in the second derivative, but it bothers me none the less. Maybe the new one has the same or similar problem but if so, it's harder to see. I like it!
ReplyDeleteHave you looked at yin-yang patterns made from overlapping cardioids? They might have the tangent properties you like. http://dl.dropbox.com/u/176875/Sights/YYC.jpg
ReplyDelete